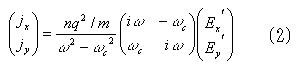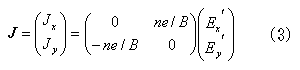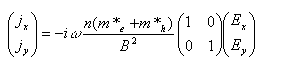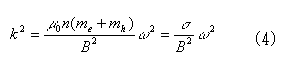サイクロトロン共鳴のドップラーシフト
通常、金属におけるサイクロトロン共鳴は金属表面1μm程度の電子だけが関係する。残りの電子は金属の表皮効果のためにマイクロ波と相互作用をすることは無い。しかし、ある条件が揃うと、強磁場下ではマイクロ波はキャリアのプラズマ運動を励起して磁気プラズマ波となって金属内を伝播できるようになる。このとき、通常は観測にかからないバルク内の電子が、サイクロトロン共鳴の観測にかかるようになり、フェルミ面に関する新たな情報をもたらしてくれる。
バルク内の電子の運動は、静磁場がかかったとき、その磁場に垂直な平面内での円運動(サイクロトロン運動)と、磁場に平行な方向の並進運動に分けて考えることが出来る。強磁場、純良試料内を伝播する磁気プラズマ波もまた、静磁場に平行に進行することになる(図1)。
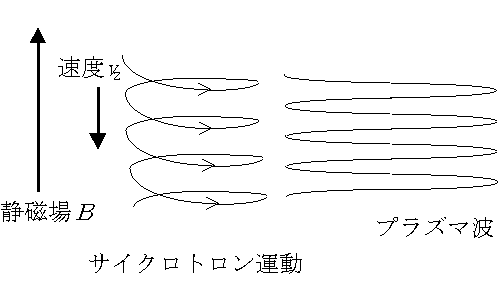
図1
このとき、静磁場方向に進む電子は、同様に静磁場方向に進行するプラズマ波の周波数をドップラーシフトした周波数で見ることとなる。
すなわち、速度±vzで進む電子は、z 軸方向に進む電磁場
E ' = Exyexp[i(kz - ωt)]
に対して、z = z' ± vzt と座標変換した電磁場を感じることとなる。これを代入すると、
E ' = Exyexp[i{k (z' ± vzt) - ωt }]
=Exyexp[i{kz' + (±kvz - ω)t }]
となり、電子は見かけ上の周波数ω ± kvzを感じる。このドップラーシフトした周波数が、キャリア自身のサイクロトロン周波数 ωC と一致したとき、共鳴条件が満たされるわけである。ドップラーシフトサイクロトロン共鳴(Doppler-shifted cyclotron resonance DSCR)が観測されるならば、その共鳴位置から電子の速度vzをダイレクトに知ることが出来る。DSCRの共鳴条件は、
ω ± kvz = ωC
で与えられる。
磁気プラズマ波自体は、極めて高品質の試料においてのみ観測される現象であり、今まではCuやBiといった純金属においてのみ観測されてきた現象である[1]。最近我々のグループにおいて、補償された半金属である希土類モノプニクタイドで磁気プラズマ波(補償された半金属ではアルフェン波と呼ばれる)に関するドップラーシフトしたサイクロトロン共鳴の観測に成功した[2,3]。
表皮効果
金属のサイクロトロン共鳴を測定する上でよく知られた現象に“表皮効果”がある。金属内の伝導電子は、マイクロ波の変動電場に合わせて素早く動くことが出来るため、その伝導電子の作る電場がマイクロ波の電場を打ち消してしまって、マイクロ波は金属内を“表皮深さ”程度しか進入することが出来ない。この事情を式で書くと、、
簡単のために金属と同程度の密度の電子ガスを考える。このとき、マックスウェルの方程式は以下で与えられる。
rotE ' = ∂B '/∂t
rotH ' = J
ここで ' は交流電磁場であることを忘れないためのものである。ここで変位電流
∂E ' /∂t
は無視している。上の式は比較的低周波(プラズマ周波数よりもずっと低い周波数)で正しい式である。プラズマ周波数以下では、変位電流はJに比べて十分小さく、マイクロ波ミリ波領域では上の式を用いてまったく問題にならない。
透磁率は真空中と変わらないとして、この2つの式からB ' = μ0H ' を消去すると、
ΔE ' - grad dive E ' = μ0∂J/∂t
(1)
である。ここで金属中を流れるJ の在り方により、伝播する波動の特性が決定される。通常はオームの法則が成り立ち、J = σ0E ' であるが、この場合には例えば z 方向に伝播する解を求めてみると
E ' = Exyexp[i(kz - ωt)]
を(1)に代入して、波数が(分散関係が)
k = (1+i)(μ0ωσ0/2)1/2
と求まる。すなわちこれは、波数 k が複素数になり、電磁場は金属中を表皮深さ
(2/μ0ωσ0)1/2
程度しか進行できないという正常表皮効果を表している。これは静磁場がない場合(拡張すればωcτ << 1)の解である。
磁気プラズマ波[1]
ωcτ >> 1(強磁場低温下)においては、状況は大きく変わってくる。磁場中では電子はサイクロトロン運動を行うので、電子の作る電流はそのことを考慮しなければならない。サイクロトロン運動は静磁場に垂直な平面に関する周期運動なので、この効果は静磁場に垂直に偏った電磁場に対して大きな影響を与える。問題になるのは、静磁場方向に垂直に偏り静磁場方向に進行する電磁波である。静磁場と電磁波の進行方向を z 軸方向として、電荷 q のキャリアに関して磁場によるローレンツ力を加えた運動方程式を解くことにより、静磁場中の電流 J として以下の表式を得る。



この式において、ωτ >> 1の条件(マイクロ波の1周期の間に電子が散乱される確率は小さいという条件)を考えると、
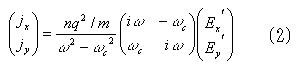
となる。この式を見ると、ω = ωcのサイクロトロン共鳴条件を満たす点は特異点で、この近辺で状況は複雑である。つまり、ω 〜 ωcの領域において正確な状況を調べることは困難である。ただ、通常問題になるのはω << ωcの領域である。これまでの仮定を整理すると、
ωcτ >> 1(強磁場低温下で、キャリアのサイクロトロン運動1周期の間に電子が散乱される確率は小さい)
ωτ >> 1(十分高周波でマイクロ波1周期の間に電子が散乱される確率は小さい)
ω << ωc (キャリアのサイクロトロン周波数がマイクロ波の周波数より十分大きい。すなわち、磁場の影響を強く受けるのはサイクロトロン周波数より低い周波数の電磁波であり、サイクロトロン周波数よりも高い周波数の電磁波は磁場の影響をあまり受けない)
ω << ωcの条件から、(2)式は、
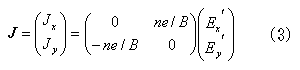
という単純な形で書き表される。これを(1)式に代入して、z 方向に伝播する解を求めてみると、z 方向に伝播する波動の解が得られる。これはヘリコン波と呼ばれる。ヘリコン波の分散関係は
ω = (B/μ0ne)k2
で表される。ヘリコン波はCuやNa等の極めてクリーンな試料において観測される。
この近似のもとでは式(3)を見るとわかるように、電荷qの符号が逆になると流れる電流Jが逆向きになる。つまりはホールと電子で、式(3)の形の電流への寄与は逆向きに打ち消しあうこととなる。しかもこの電流はキャリア密度だけで決まっているので(有効質量に依存しないので)、ホールと電子の数が等しい補償された半金属では完全に打ち消しあって0となってしまう。
補償金属において伝播するアルフェン波は(2)式に立ち返って、ヘリコン波の場合は無視していた対角項の効果である。電荷-e有効質量m*eの電子と、電荷e有効質量m*hのホールを考え、ω << ωc の近似のより高次の項まで考え、式(2)をホールと電子で足し合わせると
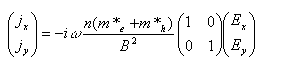
となる。この式を(1)に代入してやると、
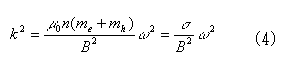
の分散関係を持つ波動が伝播することがわかる。これがアルフェン波である。
Doppler-shifted cyclotron resonance(DSCR) in LaSb[2,3]
LaSbは単純なNaCl型結晶構造を取り、キャリア密度が通常の金属より2桁ほど少ない補償された半金属である。少数キャリア系強相関物質CeP,CeSbやYbAs等の参照物質として研究されてきた。そのフェルミ面は単純であり、X点の回転楕円体電子面αブランチ、Γ点の2つのホール面βブランチとγブランチからなる。βブランチは球状であるが、γブランチはやや<100>方向に伸びた八面体状をしている。我々のグループは、そのLaSbで残留抵抗0.13μΩcmの純良試料の育成に成功した。横磁気抵抗の測定では、図2の様に、9Tでの抵抗が0磁場の9000倍にも達し、極めて純良な試料であることがわかる。

図2
この試料を用いてサイクロトロン共鳴の測定を行った。図3は B // [100] で、空洞共振器から透過してきたマイクロ波強度の磁場変化を幾つかの温度で並べたものである。低温ではスペクトルに、A, B, C, Dで示したような4つの吸収が観測された。これらの吸収は40Kで全て消滅する。40Kでも右肩下がりのスペクトルが残るが、サイクロトロン共鳴の測定は交流伝導度の測定であり、すなわちこれは図2に示した磁気抵抗の反映である。

図3
これらA, B, C, D、4つの吸収の周波数変化を取って、共鳴位置の周波数−磁場ダイアグラムとして描いたものが図4である。
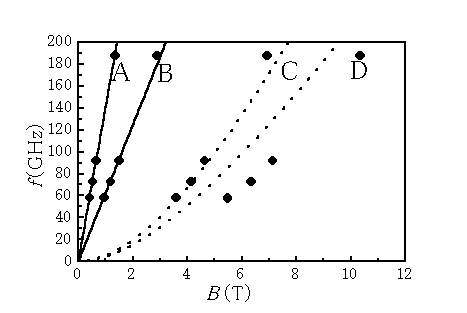
図3
図から見てわかるように、A, Bの吸収は原点を切る直線に綺麗に乗っており、これは
ωC = eB/m*CR
の磁場に対して周波数がリニアな通常のサイクロトロン共鳴の共鳴条件で表され、直線の傾きから有効質量がA, Bそれぞれ0.20m0, 0.45m0と見積もられる。これらは角度変化の測定から、それぞれαブランチ、γブランチであることがわかる[2]。
対して、C, Dの共鳴位置は、通常のリニアなサイクロトロン共鳴の共鳴条件ではあらわされず、周波数−磁場ダイアグラム上で非線形な振る舞いを見せている。また、その共鳴磁場はかなり高い磁場であり、1つの点で有効質量を評価すると、1〜3m0という相当に大きな値となってしまう。ただ、図3を見る限り、C, Dの吸収も通常のサイクロトロン共鳴とまったく同じ温度で消滅しており、この吸収もまたキャリアのサイクロトロン運動に関係した現象であることは明らかである。
ポイントは、
1.共鳴周波数−共鳴磁場の関係が非線形である
2.通常のサイクロトロン共鳴より高磁場に位置する
3.サイクロトロン運動に関係する現象である
この3つのポイントをDSCRでうまく説明することができる。共鳴磁場が高磁場に位置するというのは、見方を変えれば、電子の感じる周波数が見かけ上大きくなっていると見ることもできる。すなわち、電子から見て、周波数がドップラーシフトして大きくなるならば共鳴位置が高磁場へシフトすることとなる。非線形性は、(4)の波数が磁場依存性を持つところから出てくる。DSCRもサイクロトロン共鳴なので、当然温度の上昇で消える。
ある条件(純良試料、低温、強磁場)を満たせば、補償された半金属内には式(4)のような波数 k を持つアルフェン波が伝播できる可能性がある。今の実験では(静磁場に対してマイクロ波の変動電場が垂直)、アルフェン波の伝播方向は磁場方向にあり、アルフェン波と逆向きに最大の速度(vF)を持つ(フェルミ面の<100>方向の極の)電子が最も高磁場側へシフトし、極の点として観測にかかる[1]。
(4)式の波数 k をDSCRの共鳴条件 ω ± kvz = ωC に代入して ω で解くと、

を得る。ここでは ω + kvz = ωC を取った。もう1つの条件 ω - kvz = ωC は共鳴位置が低磁場方向へシフトすることを意味し、その領域では磁気プラズマ波は伝播できない。この式の中の σ はキャリア密度と有効質量に依存する定数であるが、LaSbのフェルミ面を考慮して書き直すと、

となる。ここで、nj, mjはそれぞれのブランチのキャリア密度と有効質量である。γブランチは球で近似している。vz はdHvA効果から見積もられるそれぞれのブランチの<100>軸方向の vF を、キャリア密度、有効質量も実験結果から見積もったものを用い、(5)式を使って計算しプロットしたのが、図3の点線である。実験結果を定性的に(半ば定量的に)説明できる。LaSbは<100>方向に4つの極を持つが(2種類のαブランチα⊥, α//、βブランチ、γブランチ)、図の点線はα//ブランチとγブランチに対応し、残りのブランチは更に低磁場側にあるので、観測にかかりにくいと考えられる。
今の見積もりでは、有効質量のパラメータが実験で十分精度良く決まっていないので、これ以上の定量的な解析は無理であるが、有効質量を完全に決定できれば、DSCRの測定からフェルミ速度 vF をダイレクトに決定することが可能である。
[1] E. A. Kaner and V. G. Skobov, Adv. Phys. 17(1968)605.
[2] M. Yoshida et al., J. Phys. Soc. Jpn. 71(2002)1752.
[3] M. Yoshida et al., Phys. Rev. B 66(2002)233107.
戻る