有限Haldane鎖の強磁場ESR
量子スピン系の問題
S = 1/2の反強磁性一次元鎖は0Kでも磁気秩序を示さないということが昔から知られている。これは古典的なイメージの↑↓↑↓という状態がハミルトニアンH = ΣJi,jSiSjの基底状態ではないので、↑↓↑↓というような秩序状態になり難い、すなわち量子効果により秩序が妨げられるということで直感的に理解される。そのような、量子効果が強く効いて古典イメージがうまく当てはまらないスピン系のことを量子スピン系と呼んでいる。一般に量子性は系の次元性が低いほど、またSの大きさが小さいほど良く効くので、一次元系、二次元系の一部、そしてS が1/2あるいは1くらいのものが量子スピン系としてくくられることになる。
↑↓↑↓というような秩序状態は直感的にわかり易く、温度を冷やしていって最終的にそういう秩序状態に落ちつくというのはすぐに納得できる話である。では、量子揺らぎによって乱されて、そういう秩序が出来ない場合に、スピンは低温で結局どういう基底状態を取るのか?という問題がある。同様のことは、三角格子やパイロクロア等のフラストレーションがある系でも考えられて、フラストレーションにより秩序化が妨げられた場合、最終的にどういう基底状態が実現するのか興味深い問題である。例えばResonating Valence Bond(RVB)やスピン液体と呼ばれるような状態が、実際の物質で実現しているか否か、実現しているのであれば、その直接的な証拠をミクロスコピックに得たいというのが、量子スピン系及びフラストレーション系の実験の、現在の最も面白い課題ではなかろうか。
不純物ドープの量子スピン系
量子スピン系における不純物ドープの研究の目的は、一つは不純物誘起の相転移を見ようという試みであるが、もう一つ、不純物により誘起された構造をミクロスコピックに直接観測することにより、そこから系の基底状態の情報を得ようとする目的がある。例えば下図左の様に低次元スピン系があったとして、その基底状態はもしかしたらスピン液体的な状態かもしれないと考えられる。ただ、そのような量子多体的な状態は時空間にゆらぎがあって実験的に直接的にとらえるのは難しい。
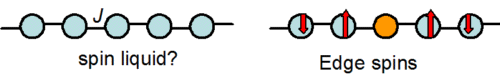
そのようなときに、図右のように不純物を導入してやると、そこで系の相関が切られ、切れた端には本来の系の相関を反映する形で端状態が出現することがある。このような端状態は、実験的に直接観測がしやすく、この構造を詳細に調べることによって、実験的に系本来の情報を直接的に得ることが可能になる。
量子スピン系の一つHaldane系
S = 1の一次元反強磁性鎖はHaldane系と呼ばれる。これはHaldaneという人が、「スピンが半整数の一次元系は励起スペクトルにgapはないが、スピンが整数の一次元系は励起スペクトルにgapを持つ」という予言をしたことでそう名づけられた[1]。基底状態から励起状態へgapがあるかどうかは、0Kでの帯磁率が0になるか(gapあり)有限値になるか(gap無し)という明確な違いとなって現れる。スピンの大きさが違うだけで、系の磁気的振る舞いが定性的にすら激変してしまうということは古典的な描像からは全く考えられないことであり、非常に注目された。実験的にもS = 1の擬一次元鎖が合成され、実際にgap(Haldaneギャップ)を持つことが観測され、Haldane予想の正しさは確立している[2,3]。
Haldane系の基底状態は現在Valence Bond Solid(VBS)の描像で理解されている。それはもともとのS = 1スピンが2つのS = 1/2スピンに分けて考えられ、そのS = 1/2のスピンが隣同士でシングレットを組むという状態である[4]。VBS状態は様々な理論・実験により確立されており、絵的に理解できるという点からもとてもユニークな、量子効果によるdisordered stateの一つである(下図)。
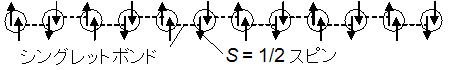
不純物ドープによる手法をHaldane系の場合で考えると、VBS状態が本当に実現されているのならば、一次元鎖をどこかで切った場合に、鎖端にSingletを組めずに余ってしまうS = 1/2のスピン自由度(端スピン)が現れることが期待される(下図参照)。もともとがS = 1のスピン鎖であるにもかかわらず、S = 1/2のスピン自由度が現れるというのは不思議な話であるが、実際に不純物ドープしたHaldane系モデル物質においてS = 1/2のスピンESR共鳴が観測され、VBS描像の正しさが実験的にも証明されている[5,6]。ここで不純物ドープは、S = 1スピンを担うのがNiであるならば、MgやZnなどの非磁性不純物を少量投入し、Niと置換してやることにより一次元鎖を切る役割を担う。
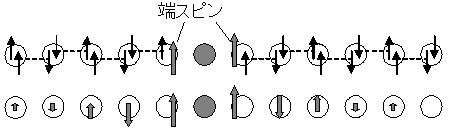
更に進んだ研究として、端状態(S = 1/2の端スピン)の鎖内へのしみ出しを観測することにより、Haldane鎖本来の相関長を見積もるという研究が行なわれた[7]。VBS状態は絵的には上で示したようにSingletの集合として描かれ、その場合鎖端に余るのは一つのS = 1/2スピンである。しかし、実際のスピン鎖の基底状態は量子多体的な状態であり、スピン間の相関が複数サイトに渡って存在しSpin Liquid Likeな側面を持っている。計算によると、スピン間の相関は絶対0度では距離に関して指数関数的に減衰し、その減衰定数はだいたい6サイト程度と見積もられている。すなわち、一次元鎖を切ってそこにS = 1/2スピン自由度が現れたならば、それは鎖内に向って6サイト分のくらいの広がりを持っているはずである。それはStaggeredモーメントとして現れ(上図下)、それによる内部磁場をNMRで観測することにより、Haldane鎖の相関長の直接的な見積もりが実験的に行なわれ、計算との良い一致が得られている[7]。
有限鎖
不純物でスピン鎖を切ると、それはただ単に切れるだけではなく、様々な鎖長の有限鎖を物質内に作り出すことになる。不純物がランダムに磁性イオンと置換するならば、鎖長がN = 1から∞までの有限鎖が簡単な確率分布に従って生成される。それらの有限鎖は、有限系として特徴的なエネルギー状態を取ることが期待でき、更に系本来の相関を反映するかたちで鎖長N依存性を持つことも考えられる。Haldane系でも、スピンの相関長が数サイトと言えどもあるわけだから、不純物ドープによってできる有限長鎖の端と端で、端状態(S = 1/2スピン自由度)同士の相互作用が期待できるはずである(下図参照)。そしてその相互作用の大きさは、鎖が長ければ長いほど小さくなってゆき、スピンの相関長よりも鎖の長さがずっと長くなるところで0に収束してゆくはずである。すなわち、有限鎖を通じた相互作用によって鎖端スピンの状態はまさにスピンの相関距離と関係する鎖長依存性を持つはずである。

Batistaの有限鎖モデル
理想的なハルデン系モデル物質であるY2BaNiO5について、Zn,Mg等の非磁性不純物をドープした系で、上で述べたような有限鎖効果が議論されてきた。Y2BaNiO5はNi2+イオンがS = 1のスピンを持ち、a軸方向に一次元鎖をなす。鎖内の交換相互作用Jとハルデンギャップはそれぞれ280 Kと100 K程度と見積もられている。またJに比べてNi2+のシングルイオン磁気異方性はD = -11 K, E = -3.6 Kと小さく、鎖間相互作用も無視できる程度なので、一次元ハイゼンベルグモデルとして理想的な物質である。Y2BaNiO5にZn,Mg等の非磁性不純物を入れた場合、ランダムにNiと置換して様々な長さの有限鎖を作り出す。不純物サイトを挟んだ相互作用は小さいとして、有限鎖を通じた相互作用だけ考慮に入れた場合、定性的に考えれば、有限鎖が短いときは端スピン同士がeffectiveな交換相互作用J'を持ってdimer化することが考えられる。鎖長Nが奇数のときはferro的なダイマーになるはずであり、Nが偶数のときはantiferrro的なダイマーになるはずである。有限鎖が長くなると両端のedge spinが互いに独立になり、2つの自由なS = 1/2スピンに収束してゆくはずである。現実の系に即した有限鎖のHamiltonianは以下の式で書かれる。
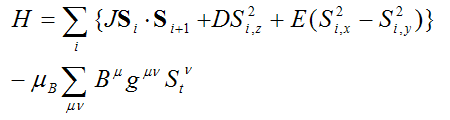 (1)
(1)
この式で、足し合わせはi = 1からNまでであり、Jは最近接反強磁性相互作用、D, EはNiのシングルイオン磁気異方性、右辺の第2項はゼーマン項(Stはtotalスピン)である。また、x, y, zはY2BaNiO5においては結晶軸のb, c, a軸に対応し、a軸がchain方向である。
Batista等はこのHamiltonianから以下のような低エネルギーeffective Hamiltonianを導入した[8,9]。
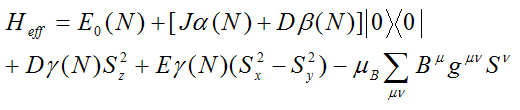 (2)
(2)
この式で、α(N), β(N), γ(N)は鎖長Nに依存するパラメータであり、Batista等のDMRG計算によるとN = 15〜30くらいで0へと収束してゆく。これは相関長6の2倍とだいたい対応している。Sはスピンオペレーターで、S = 1の |11>, |10>, |1-1>に相当する3準位あり、また|0>はSinglet状態である。(2)式をもう少しわかりやすく説明すると、有限Haldane鎖の低エネルギー状態は4つのレベルが存在し、非常に長い鎖ではそれが2つのS = 1/2スピン自由度に相当することになる。この事情はα(N), β(N), γ(N)が0に収束したときを考えれば、|11>, |10>, |1-1>と|0>の状態が0磁場では全て縮退し2つのS = 1/2スピン自由度に相当していることがわかるであろう。その上の励起はHaldane gapを超えなければ存在せず、(2)式では考慮されていない。Nが小さくてα(N), β(N), γ(N)が有限値のときは、端のS = 1/2スピン同士が相互作用し、Nが奇数のときはferro的なダイマー、Nが偶数のときはantiferrro的なダイマーになるという事情に対応し、(2)式はsinglet-triplet gapのエネルギーが[Jα(N)+Dβ(N)]で表され、更に3重項間がeffectiveなD, E項、Dγ(N), Eγ(N)で分裂するという式になる。α(N), β(N), γ(N)は奇数鎖、偶数鎖で符号が変わる。
有限Haldane鎖の強磁場ESR
Hamiltonian(2)は有限長のHaldane鎖の低エネルギーレベルが特異な鎖長依存性を持つことを示している。そして、それはまさにHaldane鎖の基底状態の量子多体性に関係しているわけである。実際、有限Haldane鎖が(2)式のような鎖長依存性を示すのかどうか、示すとしたらそのパラメータが理論とうまく合うのかどうか、実験で調べてみることは興味深い。比熱・帯磁率といったマクロな測定、および低周波なKバンド(24 GHz)ESR測定、中性子非弾性散乱測定の結果はBatista等の有限鎖モデルでコンシステントに説明がなされている[8-10]。しかしながら、それらは単に様々な鎖長の有限鎖の寄与をその確率分布で足しあわせればまずまず実験結果を説明できるということを言っているだけであって、実際に直接鎖長依存性を見ているわけではなかった。我々の結果は、共鳴法の利点を最大限に生かして、鎖長ごとにシグナルを分離して観測し、それらがまさに(2)式で表されるような鎖長依存性を持つということを示す結果である[11]。
測定はMgを4%ドープしたY2BaNiO5の単結晶試料を用い、強磁場多周波ESRをパルス磁場で温度範囲4.2〜80 K、周波数範囲 40〜420 GHzで行なった。周波数は一定に固定され、磁場を掃引することによりスペクトルが得られる。周波数―磁場が共鳴条件を満たすところで共鳴吸収が観測される。
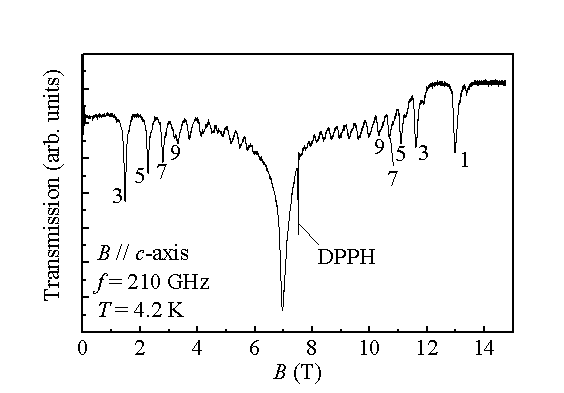
図1 周波数210 GHz、温度4.2 KにおけるESRスペクトル。図中の1,3,5,・・・の指数は有限鎖の長さNを表す。
図1は周波数210 GHz、温度4.2 K、磁場をc軸にかけたときの共鳴吸収スペクトルである。図の中央の非常に大きな共鳴吸収はg = 2.2で,周波数依存性の測定から、共鳴条件が周波数−磁場に対して原点を切る線形な直線で表されるのでS = 1/2スピンの共鳴で理解される。すなわち、鎖長が十分に長く、鎖端に生じたスピン自由度が互いに独立である有限鎖からの寄与であると考えられる。図1ではそれ以外に無数のサイドピークが観測されている。これらはまさに、鎖長が短い鎖のシグナルが、図に示した1,3,5,・・・の鎖長で分解され観測されていることがこの後に示す周波数依存性の測定から明らかになる。ここでN = 1はMg2+に挟まれた一つのNi2+イオンに相当する。数字が大きくなるほどシグナルが中央へ寄っているのは、鎖長が長くなるにつれて鎖端同士の相関が弱くなっていき、どんどんと自由なS = 1/2スピン、すなわちメインピークに近づいていくからである。鎖長が30 を超えるくらいでシグナルの分離が困難になり、それ以上長い鎖はすべてメインピークに寄与することになる。指数が奇数であるのは、偶数鎖はシングレット基底状態を取るので、低温では明確に観測されないからである。偶数鎖についても4.2 Kから温度を上昇させることでシングレットからトリプレットに励起された分のシグナルが観測できる。
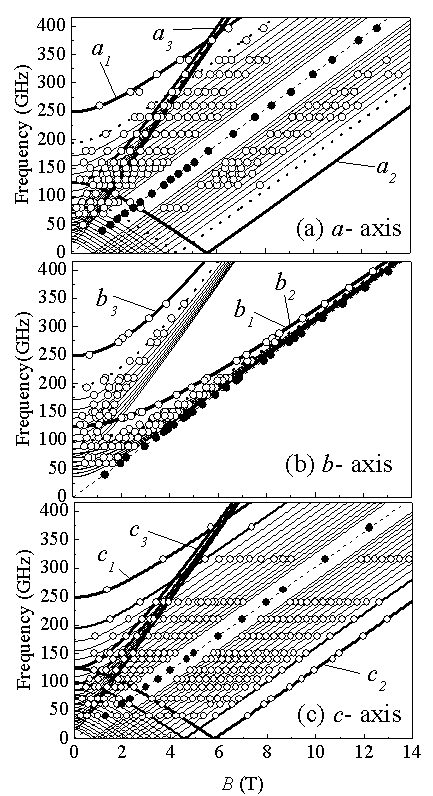
図2 周波数磁場ダイアグラム。(a),(b),(c)はそれぞれ、磁場をa,b,c軸にかけたときの結果。黒丸はメインピークの共鳴点。白丸はサイドピークの共鳴点。
周波数範囲 40〜420 GHzの間で多周波数の測定を行い、シグナルの位置を周波数−磁場の関係でプロットしたのが図2である。測定はa,b,cの3軸に関して行った。図中でメインピークの共鳴点(黒丸)はすべての軸方向で原点を通る直線(破線)に載っている。それ以外に、サイドピークの共鳴点(白丸)が無数に存在し、それぞれの軸方向で特異な周波数依存性を見せている。これら無数のサイドピークの共鳴点全てを、有限鎖モデルのハミルトニアン(1)で見事に説明することができる。ハミルトニアン(1)の2行目の式は単純にシングルイオン磁気異方性を有するS = 1のスピンハミルトニアンの形である。奇数鎖の場合、シングレットは励起状態になるので、このS = 1のスピンハミルトニアンだけを考えればよくて、一般にD, E項で分離したS = 1スピンは各軸に関して3つのESR遷移がある。図2の太線はそのai,bi,ci (i = 1,2,3)のESR遷移の周波数−磁場モードを一組のD(= -8.97 K),E(= -2.98 K)項を用いて計算したものである。太線は0磁場でもっとも大きな周波数ギャップを持つモードを描いていている。(1)式において,N = 1のときγは1になるはずであり、このとき有効的な異方性Dγ(N), Eγ(N)は本来のNi2+のD,E項と一致して絶対値で最大値をとるはずである。それがまさに太線のモードであり、N = 1 (孤立Ni2+)の共鳴モードである。得られるD(= -8.97 K),E(= -2.98 K)はドープされていないY2BaNiO5から求められた値とよくあっている.それよりももう少しDγ, Eγが小さい点線のモードはN = 3の共鳴モードである。その他の白丸も全てγを小さくしていったときの共鳴モード(細線)でフィットできる。このようにして、(1)式を用いて全ての共鳴が理解される。フィッティングパラメータはγ(N)のみであり、この鎖長依存のパラメータがN = 1から27まで精密に決定される。得られたパラメータはBatista等のDMRG計算と比較することが出来る。それを図3に示す。
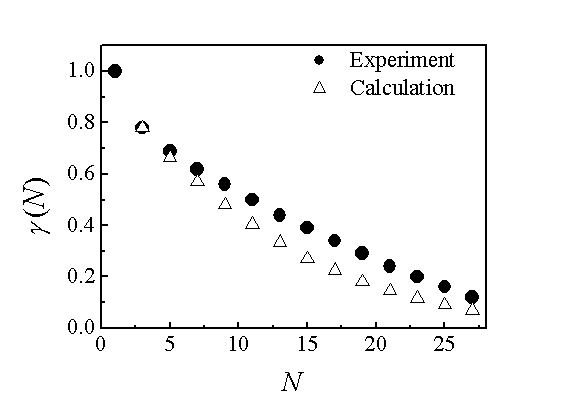
図3 γの鎖長N依存性。黒丸が実験により得られた値で、白三角は計算値。
実験で得られたパラメータは理論計算と定性的によくあっているが、鎖長が5以上で若干実験値のほうが大きくなっている。実験データは0.2 Kくらいのエネルギー差も分離できているので、非常に高い精度を持っている。計算はE = 0として を計算しているので、もう少し洗練されたモデルが必要なのかもしれない。鎖端同士の相関は異方性の情報として30サイトまで及んでおり、ハルデン鎖の相関長6の2倍よりだいぶ長いが、その辺の物理的意味は今後検討の余地がある。シングレット−トリプレットギャップの大きさを決定付けるパラメータα(N)はDMRG計算によると相関長6の2倍を直接反映した振る舞いを示しているので、実験でもより緻密に温度変化測定を行い、α(N)及びβ(N)の情報を得ることは今後の課題である.
以上見てきたように、スピン系に不純物を導入し、その周辺構造をESRやNMRといったミクロな測定手法で調べることは、系本来の性質を明らかにする上で非常に強力な手法である。特に、理想的な有限鎖が出来る場合、少数系の数値計算と精密に比較可能なので、理論の妥当性を調べるのに非常に便利である。今後、様々な系で、こういった手法が適用されていくことが期待される。
[1] F. D. M. Haldane, Phys. Rev. Lett. 50, 1153 (1983).
[2] K. Katsumata, H. Hori, T. Takeuchi, M. Date, A. Yamagishi, J. P. Renard, Phys. Rev. Lett. 63, 86 (1989).
[3] Y. Ajiro, T. Goto, H. Kikuchi, T. Sakakibara, T. Inami, Phys. Rev. Lett. 63, 1424 (1989).
[4] I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki, Phys. Rev. Lett. 59, 799 (1987).
[5] M. Hagiwara, K. Katsumata, I. Affleck, B. I. Halperin, and J. P. Renard, Phys. Rev. Lett. 65, 3181 (1990).
[6] S. H. Glarum, S. Geschwind, K. M. Lee, M. L. Kaplan, and J. Michel, Phys. Rev. Lett. 67, 1614 (1991).
[7] F. Tedoldi, R. Santachiara, and M. Horvatic, Phys. Rev. Lett. 83, 412 (1999).
[8] C. D. Batista, K. Hallberg, and A. A. Aligia, Phys. Rev. B 58, 9248 (1998).
[9] C. D. Batista, K. Hallberg, and A. A. Aligia, Phys. Rev. B 60, R12553 (1999).
[10] M. Kenzelmann, G. Xu, I. A. Zaliznyak, C. Broholm, J. F. DiTusa, G. Aeppli, T. Ito, K. Oka, and H. Takagi, Phys. Rev. Lett. 90, 087202 (2003).
[11] M. Yoshida, K. Shiraki, S. Okubo, H. Ohta, T. Ito, H. Takagi, M. Kaburagi, and Y. Ajiro, Phys. Rev. Lett. 95, 117202 (2005).
戻る
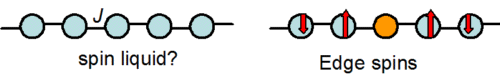
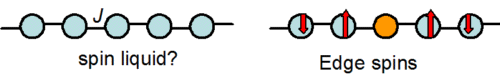
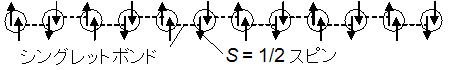


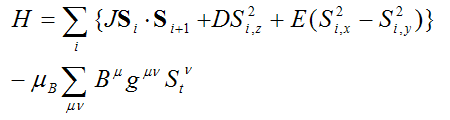 (1)
(1)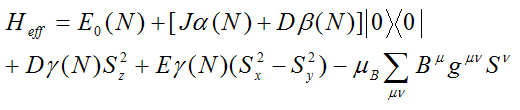 (2)
(2)

